DC and AC Force of a Gapped EI-Core Inductor
David Meeker
dmeeker@ieee.org
Companion file: induct1a.fem
Introduction
This is a companion example to the Inductance Calculation Example on the FEMM website. The objective is to demonstrate how forces are computed in FEMM, and to show how forces differ when computed in AC and DC problems.
Example Geometry
As in the Inductance Calculation Example, the geometry is composed of a gapped, laminated EI core with the cross-section as pictured in Figure 1. An E core has a center pole 0.5" wide and outer poles 0.25" wide. It is assumed that the core extends for 1" in the into-the-page direction, so that the center pole has an area of \(a\) = 0.5 in2. An air gap of \(g\) = 0.025" thick separates the E from its I-shaped return path.
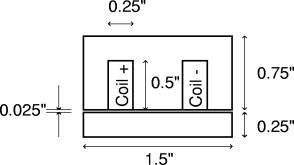
Figure 1: Example Geometry
The winding that lies in the slots of the E consists of \(n\) = 66 turns of 18 AWG wire heavy build insulation, for approximately a 66% copper fill fraction in the coil window. For the purposes of this model, the material is assumed to be a linear ferromagnetic material with a relative permeability of 2500.
Circuit Theory Force
If we assume that there is no leakage and fringing, and that the contribution of the iron sections to the reluctance of the magnetic circuit is trivial in comparison to the contributions from the air, the force on the E-core is described by: \[F = \frac{\mu_o a n^2 i^2}{4 g^2}\] If there is a 1Adc current in the wire, the calculated DC force is:
\(F\) = 1.09478 N
In FEMM, everthing is Peak, not RMS. More specifically, for AC problems, all quantities (currents, fluxes, etc.) are represent as complex numbers where the absolute value of the number represents the amplitude, and the argument of the numbers represent phase shift. For example, if \(i_{ac}\) was a complex number representing the AC coil current, we could explicitly represent current as a function of time, \(i(t)\), using the equation: \[i(t) = \mbox{Re} \left[ i_{ac} \left( \cos{\omega t} + j \sin{\omega t} \right) \right] = \mbox{Re}(i_{ac}) \cos {\omega t} - \mbox{Im}(i_{ac}) \sin{\omega t} = \mbox{Re} \left[i_{ac} \, e^{j \omega t} \right] \] For the purposes of this example, we can assume that \(i_{ac}\) is strictly real, such that: \[i(t) = i_{ac} \cos{\omega t}\] Substituting into the force equation, we get: \[F = \frac{\mu_o a n^2}{4 g^2}( i_{ac} \cos{\omega t})^2 = \frac{\mu_o a n^2 i_{ac}^2}{4 g^2} \left( \frac{1}{2} + \frac{1}{2} \cos{2 \omega t} \right) \] Substituting parameters into the equations yields:
\(F\) = 0.547391 N + 0.547391 N \(*\cos{2 \omega t}\)
Because FEMM uses a Peak convention, rather than an RMS convention, numerically the same current produces, in this example, exactly half the DC force that would be produced in the DC case, plus a 2 ω component of force of the same amplitude. When the two components of force are combined, we get a force that varies in time between zero and the DC force. The relationships between the AC and DC forces are shown graphically in Figure 2.
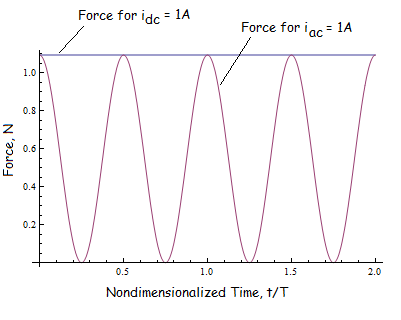
Figure 2: Force vs. Time for the same coil current under AC and DC excitation
Finite Element DC Force
Two methods of computing force are through the "Weighted Stress Tensor" block integral and through the 'Maxwell Stress Tensor" line integral. The Weighted Stress Tensor is the recommended method. It is easier to select the regions upon which the force is to be computed (i.e. simply click on the desired blocks), and the force calculation tends to be a bit more accurate because it's a 2D integral instead of a line integral. For reference, an implementation of the WST block integral is shown in Figure 3 and an implementation of the MST line integral is shown as Figure 4. In this case, very similar forces are computed by each method: 1.11347 N for WST and 1.11289 N for MST. Both calculations are a reasonable match to the circuit theory prediction of 1.09478 N.
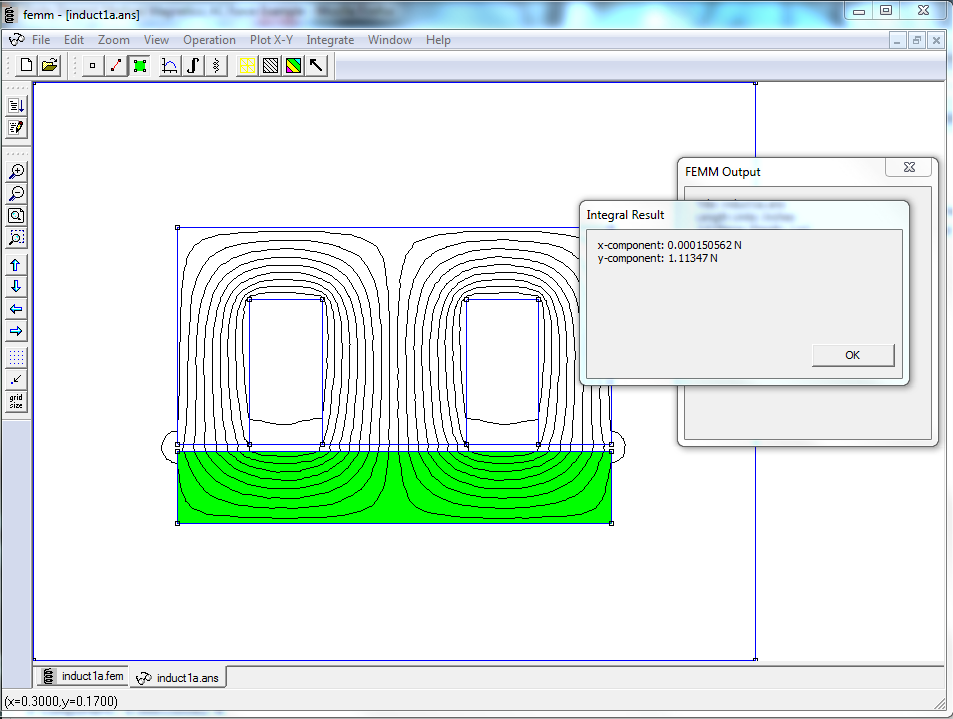
Figure 3: Weighted Stress Tensor block integral force calculated on I-section (recommended).
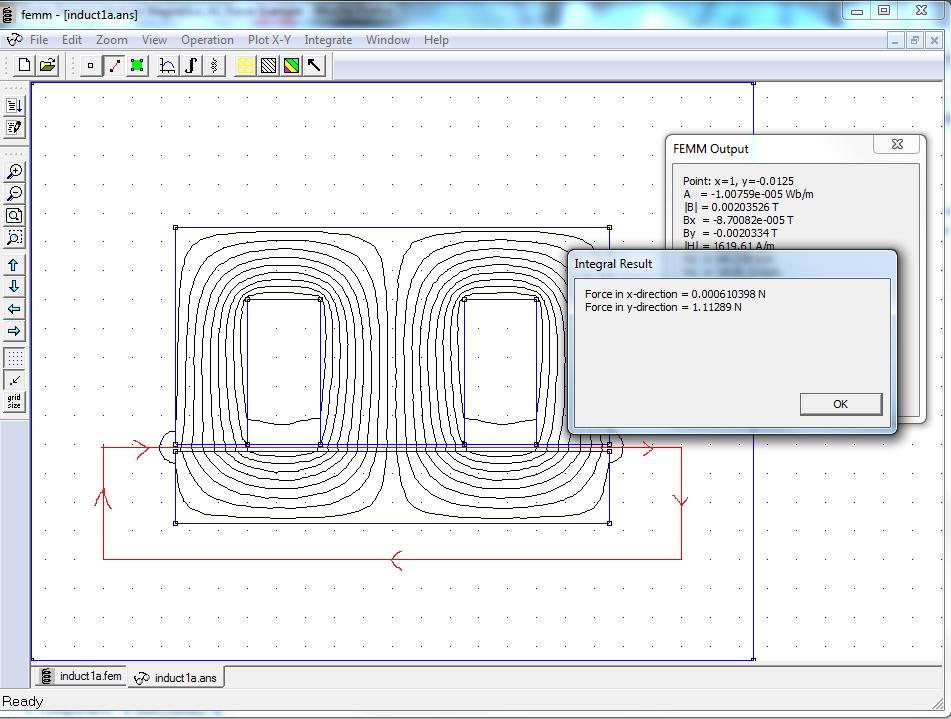
Figure 4: Maxwell Stress Tensor line integral force calculated on I-section (not recommended).
Finite Element AC Force
The problem was simulated a second time, changing the frequency from 0 Hz to 60 Hz on the Problem Definition dialog. In each case, a steady-state force of just about 1/2 of the DC value is computed, with an 2X frequency force of very nearly the same amplitude. The force calculation results are summarized in Table 1. A small but non-negligible complex component exists in the 2X part of the force due to proximity effect eddy currents in the coil's windings, implying that the eddy currents cause a slight shift in time of the peak force. Figures 5 and 6 depict the AC force calculations for the WST block integral and MST line integral, respectively.
| DC Force Component | 2X Force Component | |
| WST | 0.556734 N | 0.55673-j1.77579e-5 N |
| MST | 0.556793 N | 0.556793 N -j1.81824 N |
Table 1: AC force calculation results.
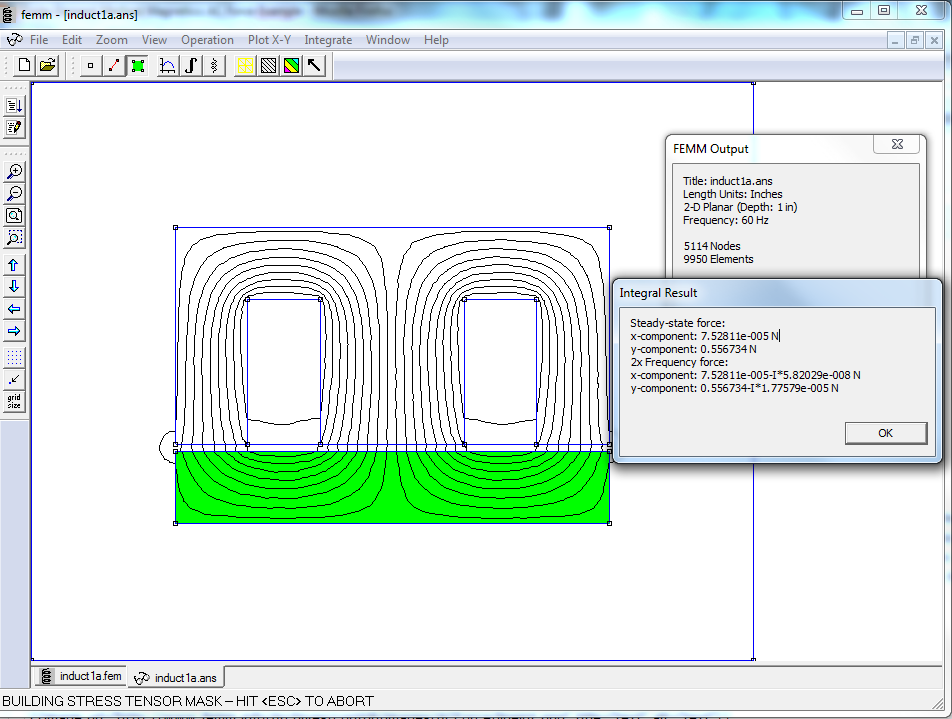
Figure 5: AC Weighted Stress Tensor block integral force calculated on I-section.
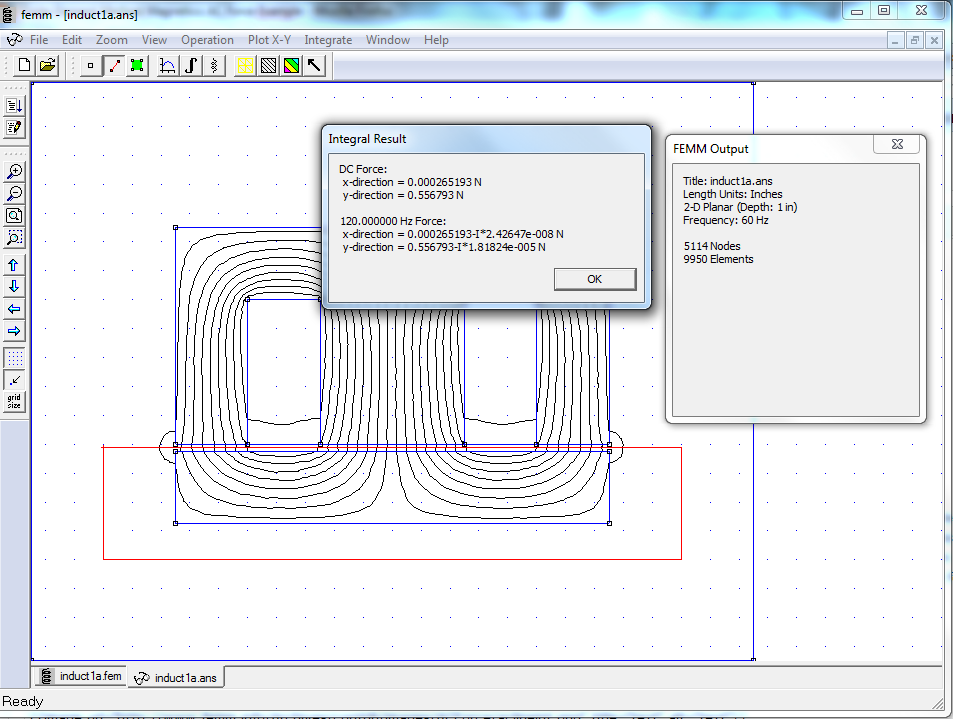
Figure 6: AC Maxwell Stress Tensor line integral force calculated on I-section.
Conclusions
This example demonstrates how forces are calculated in FEMM under DC and AC conditions. Care must be taken to remember that FEMM assumes a Peak scaling (rather than an RMS scaling) of all simulation quantities to properly interpret the force results under AC conditions.