A Rapid Procedure for Three-Phase Squirrel Cage Induction Motor Finite Element Analysis Using Magneto-Static Formulation.
Matteo Carbonieri, Nicola Bianchi
July 15, 2021
1 Introduction
This article presents a procedure to rapidly analyze the Induction Motor (IM) by performing only Magneto-Static (MS) Finite Element (FE) simulations. The nature of the IM perfectly fits in with the Time Domain (TD) analysis [1], which allows to carefully consider the saturation and compute the rotor cage induced currents. The cost of highly accurate FE analyses is the long simulation time: also if the stator current and rotor speed are known, several electric periods need to be simulated to obtain the rotor current steady state1.
The common approach for the IM analysis is based on the equivalent circuit, which parameters are computed using Finite Element Analysis (FEA). The saturated magnetizing inductance is derived from the no-load test and the rotor parameters from the locked rotor simulation [2]. This hybrid method allows a rapid analysis of the machine with lower accuracy with respect the TD approach. As a manner of fact, only the no-load saturation is considered, neglecting the effect of the load current.
The idea described in this article is to simulate the IM by imposing both stator and rotor currents as field sources in MS simulations. This target requires a strict connection with the \(dq\) analytical model of the machine to identify the position of the rotor current space vector and a FEA iterative procedure to compute the correct amplitude of the current in each bar [3–5]. This approach allows to obtain a picture of the on-load behavior of the motor and the iron saturation is determined by both magnetizing and torque currents. The IM analysis using MS simulations has the advantage of performing direct on-load tests of the motor, without the use of any equivalent circuit with previously computed parameters. The on-load saturation is better considered than in the equivalent circuit approach, since both stator and rotor currents are impose to obtain the on-load field solution. Furthermore, the method performs only MS simulations with significantly reduced computation time with respect the TD approach.
This new analysis system is deeply connected to the \(dq\) model of the IM making the procedure similar to that adopted for synchronous machines. The description of the analytical \(dq\) model of the IM is reported to list the main equations and concepts, useful for the FEA procedure. In particular, the IM model in the Rotor Field Oriented (RFO) reference frame is adopted.
The following part concerns the rotor equivalent winding definition. This tool is fundamental for a correct definition of the current in the rotor bars. Then, the full description of the analysis procedure is reported.
2 Equivalent Three-Phase Rotor Winding
Let us consider a cage IM. This particular type of rotor winding can be imagined as a poly-phase winding in which each bar represents a different phase. The on-load behavior of the three-phase IM is characterized by the slip between the stator magnetizing field and the rotor. The relative motion between the magnetizing field and the rotor bars defines the operation of this kind of electrical machine.
In the instant time \(t\), \(ω_{sl}\) is the relative mechanical-electrical speed between the stator field and the rotor, in electric radians per second. Considering a sinusoidal airgap flux density distribution, the induced voltage, at the terminals of each rotor bar, can be expressed as:
\[ \label{eq1} \begin{eqnarray}
e_1(t) & = & B_{3ph1} \sin{ \left( \omega_{sl} t \right) } L_{stk} \frac{D_i}{2} \omega_{sl} \\
& \vdots & \\
e_{Qr}(t) & = & B_{3ph1} \sin{ \left[ \omega_{sl} t - \left( Q_r - 1 \right) \alpha_r^e \right]} L_{stk} \frac{D_i}{2} \omega_{sl}
\end{eqnarray}\] where \(\alpha_r^e\) is the electrical rotor slot angle, \(Q_r\) is the rotor slot number, \(D_i\) and \(L_{stk}\) are the inner diameter and the stack length. Rotor bar currents can be written as following:
\[ \label{eq2} \begin{eqnarray}
i_1(t) & = & B_{3ph1} \sin{ \left( \omega_{sl} t -\phi_r \right) } \frac{D_i L_{stk} \omega_{sl} }{2 \left| \dot{z}_{bar} \right| } \\
& \vdots & \\
i_{Qr}(t) & = & B_{3ph1} \sin{ \left[ \omega_{sl} t - \left( Q_r - 1 \right) \alpha_r^e - \phi_r \right]} \frac{D_i L_{stk} \omega_{sl} }{2 \left| \dot{z}_{bar} \right| }
\end{eqnarray}\] where \(\dot{z}_{bar} = | \dot{z}_{bar}| e^{j \phi_r}\) is the equivalent bar impedance \(\dot{z}_{bar}\), that takes into account the presence of cage short-circuit rings.
In Figure 1a it is shown that, when only the main harmonic of air-gap flux is considered, spatial behavior of induced voltages and currents, in the rotor bars, exhibits a sinusoidal waveform. The corresponding time phasor representation is reported in Figure 1b.
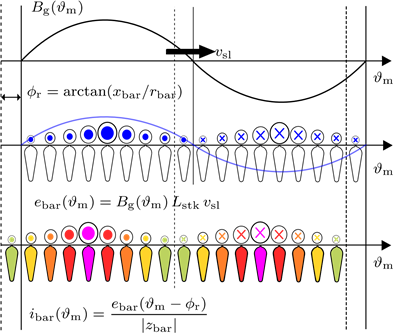
(a) Induced voltage and current spatial distribution in the slots of a squirrel cage rotor. In the drawing, \(v_{sl}\) indicates the relative speed between the air-gap flux density and the rotor, in meters per second; \(\alpha_e^r\) is the rotor slots electrical angle.
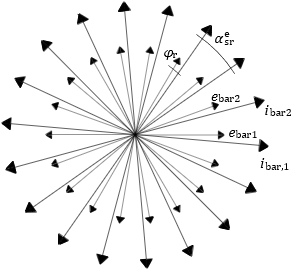
(b) Induced voltage and currents time phasors representation.
Figure 1: The induced voltage and currents in the rotor bars are represented from the spatial point of view (Figure 1a) and with the corresponding time phasors (Figure 1b).
An interesting trick is considering a three-phase rotor equivalent winding sinusoidally distributed in the rotor slots. Figure 2a shows a sketch of such a three-phase rotor winding. The size of the slot current symbol indicates the theoretical conductor density belonging to each phase within the rotor slots, that is sinusoidally distributed, per each phase, along the rotor periphery. This equivalence comes from the fact that the rotor replies to the stator magnetizing flux with a rotating Magneto Motive Force (MMF) with the same number of poles as the stator inducing field. Thus, from the stator point of view, the rotor behavior is the same as a common three-phase winding.
At first, the equivalent rotor winding definition makes easier the machine model construction, since the rotor has the same nature of the stator and it is more intuitive to derive the voltage equation for the rotor circuits. Further, this approach is very important for the machine simulations.
I order to perform MS FEA of the IM, it is necessary to properly impose the currents inside the bars. This tool makes this operation quite immediate, and also the computation of the rotor flux linkage in straightforward using an equivalent winding.
In a sinusoidal winding, the phase conductors are sinusoidally distributed in the several slots; further, each slot is filled with conductors belonging to each phase.
The vectors \(k_{ra}\), \(k_{rb}\) and \(k_{rc}\) define the fill factor of any rotor slot, according to a given phase:
\[ \label{eq3} \begin{eqnarray}
k_{ra,i} & = & \sin \left( \alpha_r^e/2 + \alpha_r^e (i-1) \right) \\
k_{rb,i} & = & \sin \left( \alpha_r^e/2 + \alpha_r^e (i-1) -2 \pi /3\right) \\
k_{rc,i} & = & \sin \left( \alpha_r^e/2 + \alpha_r^e (i-1) - 4 \pi / 3\right)
\end{eqnarray} \]
where \(i=1, \ldots , Q_r\). The rotor winding factor is computed as following:
\[ \label{eq4}
k_{wr} = \frac{\sqrt{\left( \sum_{i=1}^{Q_r} k_{ra,i} \cos \left( \frac{2i-1}{2} \alpha_r^e\right) \right)^2 + \left( \sum_{i=1}^{Q_r} k_{ra,i} \sin \left( \frac{2i-1}{2} \alpha_r^e\right) \right)^2}}{\sum_{i=1}^{Q_r} k_{ra,i}}
\]
Theoretically, the winding factor of a sinusoidally distributed winding is equal to π/4.
The number of conductors per phase of the rotor winding is fixed in order to have the same number of effective conductors as the stator winding:
\[ \label{eq5} N_r k_{wr} = N_s k_{ws} \]
where \(N_s\) is the number of conductors per phase of the stator winding and \(k_{ws}\) is the stator winding factor. The equivalence (5) accounts to facilitate the parameter estimation of the equivalent circuit. The number of series conductors per phase in each rotor slot results in:
\[ \label{eq6}
\begin{eqnarray}
n_{csr,a} & = & \frac{N_r}{\sum_{i=1}^{Q_r} k_{ra,i}} k_{ra} \\
n_{csr,b} & = & \frac{N_r}{\sum_{i=1}^{Q_r} k_{rb,i}} k_{rb} \\
n_{csr,c} & = & \frac{N_r}{\sum_{i=1}^{Q_r} k_{rc,i}} k_{rc}
\end{eqnarray}
\]
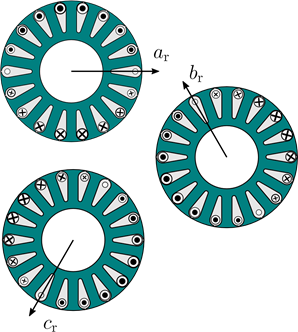
(a) Sketch of the three-phase equivalent rotor winding.
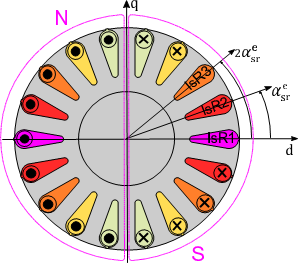
(b) Rotor current distribution with three-phase current supplying.
Figure 2: Three-phase rotor current arrangement and peripheral current distribution considering a common three-phase current supply.
The condition (5) makes the stator and rotor to have the same effective conductors per phase. This means that, having also the same magnetic circuit, the two windings produce the same magnetizing flux, when supplied by the same magnetizing current. Further, the synchronous inductances are almost the same. They differ only from the leakage component due to the different harmonic content of the two MMF and the different number of slots and slot shape. On the other hand, the magnetizing component is the same:
\[ \label{eq7} \begin{eqnarray}
L_{ms} & = & \frac{3}{\pi} \mu_o \left( \frac{N_s k_{ws}}{2p}\right)^2 \frac{D_i L_{stk}}{g'} \\
L_{mr} & = & \frac{3}{\pi} \mu_o \left( \frac{N_r k_{wr}}{2p}\right)^2 \frac{D_i L_{stk}}{g'} \\
\end{eqnarray} \]
Thus, the stator and rotor three-phase inductance are:
\[ \label{eq8} \begin{eqnarray}
L_s & = & L_{ms} + L_{\sigma s} \\
L_r & = & L_{mr} + L_{\sigma r}
\end{eqnarray} \]
with \(L_{\sigma_s}\) and \(L_{\sigma_r}\) the leakage components. Considering the hypothesis (5) and from (7):
\[ \label{eq9} L_{ms} = L_{mr} = M \]
where \(M\) is the three-phase mutual inductance between stator and rotor.
3 IM Equivalent Model
The definition of the rotor equivalent winding allows the squirrel cage IM to be considered as a three-phase shorted circuited wound rotor machine. Steady state stator and rotor voltage vector equations are:
\[ \label{eq10} \begin{eqnarray}
\vec{v}_s & = & R_s \vec{i}_s + j \omega_s \left( L_s \vec{i}_s + M \vec{i}_r \right) \\
0 & = & R_r \vec{i}_r + j \omega_s \left( L_r \vec{i}_r + M \vec{i}_s \right) -j \omega_{me} \left( L_r \vec{i}_r + M \vec{i}_s\right)
\end{eqnarray}\]
Introducing the slip: \( s = (\omega_s - \omega_{me})/\omega_s\), rearranging the rotor voltage equation, it becomes:
\[ \label{eq11} 0 = \frac{R_r}{s} \vec{i}_r + j \omega_s \left( L_r \vec{i}_r + M \vec{i}_s \right) \]
The first of (10) and (11) are linked with the equivalent circuit in Figure 3.
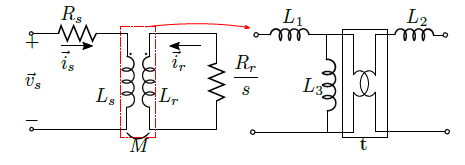
Figure 3: The steady-state circuital model of IM, with the mutual coupling between stator and rotor highlighted. It is possible to model it using a grid of inductances with the ideal transformer.
The mutual coupling can be modeled using a grid of inductances, introducing the ideal transformer, and the following relationships can be derived:
\[ \label{eq12} L_1 = L_s − t M; \;\; L_2 = L_r − \frac{M}{t}; \;\; L_3 = t M \]
The arbitrary constant \(t\) can be chosen to obtain different forms of the IM equivalent circuit.
3.1 Inverse-Γ form of the equivalent circuit and IM model in RFO reference frame
The inverse-Γ form of the IM equivalent circuit [3, 6] is derived setting to zero the inductance L2 in the model in Figure 3.
\[ \label{eq13} L_1 = L_s - \frac{M^2}{L_r}= L_t; \;\; L_2=0; \;\; L_e = \frac{M^2}{L_r} = L_φ \]
The ideal transformer constant \(t\) becomes a ratio of inductances: \(t = M/L_r\). In the inverse-Γ equivalent circuit, shown in Figure 4, Lt is the overall leakage transient inductance. The mutual magnetizing flux linkage (referred to the stator) is determined by the stator current isq flowing in the magnetizing inductance \(L_φ\).
Using the inverse-Γ IM model, the overall rotor flux space vector is due only to the \(d\)-axis stator current and the torque depends upon the \(q\)-axis current, once the rotor flux has been created. In the RFO reference frame, the rotor flux space vector lies along the \(d\)-axis and the \(q\)-axis component is equal to zero, that is the RFO condition, i.e. \(\lambda_{rd} = \lambda_r\) and \(\lambda_{rq} = 0\). From relationships:
\[ \label{eq14} \lambda_{rq} = L_r i_{rq} + M \, i_{sq}; \;\; 0 = \frac{R_r}{s}i_{rd} - \omega_s \lambda_{rq} \]
imposing \(\lambda_{rq} = 0\), it can be achieved:
\[ \label{eq15} i_{rq} = - \frac{M}{L_r} i_{sq}; \;\; i_{rd}=0 \]
Stator \(dq\) voltage equations in in the RFO reference frame are:
\[ \label{eq16} \begin{eqnarray}
v_{sd} = R_s i_{sd} - \omega_s L_t i_{sq} \\
v_{sq} = R_s i_{sq} + \omega_s L_t i_{sd}
\end{eqnarray} \]
and the rotor voltage equation is unique:
\[ \label{eq17} 0 = \frac{R_r}{s} i_{rq} + \omega_s M i_{sd} = \frac{R_r}{s} i_{rq} + \omega_s \lambda_{rd} \]
The stator \(dq\) flux linkages are given by:
\[ \label{eq18} \lambda_{sd} = L_s i_{sd} ; \;\; \lambda_{sq} = L_t i_{sq} \]
and the rotor flux linkages are expressed as:
\[ \label{eq19} \lambda_{rd} = M\, i_{sd}; \;\; \lambda_{rq} = 0 \]
From (17) the rotor slip angular frequency can be derived as:
\[ \label{eq20} \omega_{sl} = s \omega_s = - \frac{R_r i_{rq}}{\lambda_{rd}} = p \frac{P_{Jr}}{T_{dq}} \]
where the torque expression in the RFO reference frame is:
\[ \label{eq21} T_{dq} = \frac{3}{2} p \lambda_{rd} i_{rq} \]
or, alternatively, it can be expressed using the stator flux linkage and current:
\[ \label{eq22} T_{dq} = \frac{3}{2} p \left( \lambda_{sd} i_{sq} - \lambda_{sq} i_{sd} \right) \]
In Figure 4, the RFO equivalent circuit of the IM is reported. The scheme shows also the connection with the FEA model: once the stator and rotor currents are determined (with the procedure in the following section), the stator and rotor flux linkages are computed directly from the MS FEA. Finally, in Figure 5, the space vector diagram of the machine is reported.
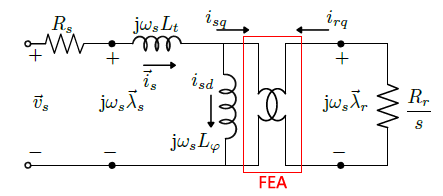
Figure 4: Steady-state equivalent circuit, according to the RFO reference frame equations. The magnetic coupling between stator and rotor is determined by FEA.
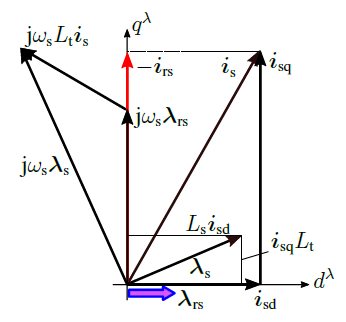
Figure 5: Space vector diagram of the IM analyzed using the RFO \(dq\) reference frame.
4 Magneto-static on-load analysis
The aim of this section is to describe a method for performing MS FEA of any on-load working point of the IM. The core of the procedure is the rotor current computation. For this purpose, several techniques have been developed. Some of them are more general, and work out any type of IM; other techniques are much faster, but just fit for open rotor slot IMs.
The analysis strategy presented in this work, has to be an effective alternative to the common techniques for the IM computation. In particular, the TD analysis, proposed by many commercial software, is a very accurate tool, but it takes a very long computational time.
The method presented here is based on the static formulation of the FE problem, that has an inherently fast convergence. The key is that the rotor induced current directly set inside the rotor bars as field sources, together with the stator current.
For this purpose, a close connection between the analytical and FE model is necessary. The adopted model as reference in the inverse-Γ model introduced in the previous section, referred to the space vectors. Actually, this model is nothing more than a simple and clear point of view for the machine currents and fluxes vector relationships. In Figure 6, the basic inverse-Γ model of the machine is reported. In red, the circuit parts, that are also modeled in FEA, are highlighted.
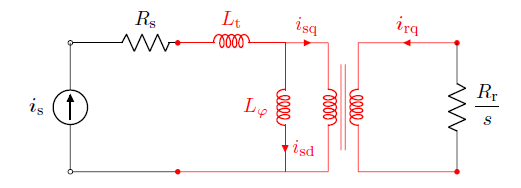
Figure 6: IM equivalent circuit, adopted to be linked to FEA. The red parts of the circuit are modeled also in FEA.
The interesting part of adopting the model in Figure 6, and the ideas behind it, is that the general approach becomes similar to a synchronous machine. In fact, the \(d\)-axis current is the flux current, which produces the rotor flux linkage; on the contrary, the \(q\)-axis currents are involved in the torque production.
The strategy presented below, is meant for analyzing the steady state operation of the IM. For this reason, as demonstrated in the previous section, the rotor \(d\)-axis current is equal to zero. The current \(i_{rq}\) is related to the stator current amplitude, from (15).
The FEA plays an important role in the determination of the rotor current amplitude, that actually depends upon the saturation state of the machine, since the inductances in (15) are deeply influenced by the iron saturation. In this way, the FE model is fundamental to carefully take saturation into consideration.
In general, fixed the stator current, the procedure for the rotor current computation is rather fast and few simulations are needed. The short computational time represents an important advantage with respect the TD approach.
A fundamental tool to generalize the procedure to any type of motor, is the equivalent poly-phase rotor winding, in case of cage induction motors. The full description of this tool is reported in section 2.
Finally, it is important to underline that the approach introduced in this section is valid only for the first harmonic of the rotor current distribution.
4.1 reference frame adopted for FEA and the link with the analytical model
At this moment, let’s consider a single position od the rotor with respect the stator, and image to analyze a single time instant of the on-load behavior. The stator current is fixed in the space and the rotor current has to be computed. Further, in Figure 7, the rotor winding is represented as a uniformly distributed winding for sake of simplicity2.
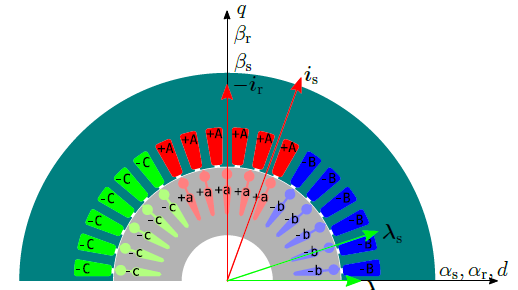
Figure 7: \(dq\) reference frame adopted for simulations. The reference space vector diagram is also reported, with the rotor flux and current space vectors in quadrature lying along the \(d-\) and \(q\)-axis.
In the time instant represented in Figure 7, the stator and rotor αβ systems are one over the other. The definition of the synchronous \(dq\) reference frame the fundamental first step of the procedure. For sake of convenience, it overlaps the αβ reference frame.
In order to apply the rotor current computation procedure, the stator \(d\) and \(q\) current components have to be known. The first information about the rotor current is that the related space vector lies along the \(q\)-axis. On the other hand, the amplitude has to be computed in order to verify \(\lambda_{rq} = 0\), that is the characteristic condition of the inverse-Γ model.
Before starting, it is important to remark that in the following particular procedure, the rotor current distribution within the rotor slots is considered uniform. It is the same as neglecting the effect of the rotor frequency on the current crowding inside the slot. This is a reasonable hypothesis considering the normal behavior of the IM at a low slip.
4.2 iterative procedure
This procedure is based on an iterative correction of the rotor current irq amplitude, until the condition \(\lambda_{rq} = 0\) is reached.
In the following, only cage IMs will be considered. For this reason, the equivalent rotor sinusoidal winding has to be defined according to the procedure outlined in section 2. With the hypothesis of having the same number of effective turns in the stator and rotor three-phase winding, the magnetizing components of \(L_s\) and \(L_r\) are the same and equal to the three-phase mutual inductance introduced in (8) and (9).
The analytical relationship between the stator and rotor current is the following:
\[ \label{eq23} i_{rq} = -\frac{M}{L_r} i_{sq} \]
where \(L_r = L_m+L_{σr}\). Generally, the leakage inductance Lσr is much lower than the magnetizing component \(M\), thus, for the first iteration of the method, the rotor current can be approximated as:
\[ \label{eq24} i_{rq,1} = -i_{sq} \]
Before starting the description of the method, it is important to highlight, that the \(q\)-axis of an IM basically has a linear behavior, during the iterative procedure. The general law (24) implicates that, the MMF along the \(q\)-axis is almost equal to zero. Actually, the currents along this axis produces only leakage fluxes, as shown in Figure 8, with a negligible iron saturation.
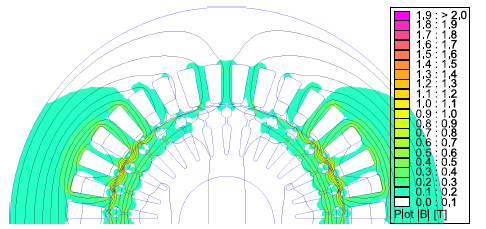
Figure 8: Flux produced by the interaction between stator and rotor \(q\)-axis currents. It is a leakage flux.
For this reason, generally, only three iterations are needed to get the rotor current amplitude that brings to zero the rotor q-axis flux linkage. So, the stator \(d\)- and \(q\)-axis currents are already know, thus the first iteration imposed current space vectors are:
\[ \label{eq25} \begin{eqnarray}
i_s & = & i_{sd} + j i_{sq} \\
i_{r,1} & = & −j i_{sq}
\end{eqnarray} \]
In Figure 9, the first iteration field solution is reported. It is evident that the flux lines within the rotor are not parallel to the d-axis, meaning that the \(d\)-axis rotor flux is not equal to zero. Further, in the field solution, also the current density is plot, to show the sinusoidal current distribution along the rotor periphery. It is clear that the direction of the rotor current space vector indicates also the spatial direction of the first harmonic of the rotor MMF.
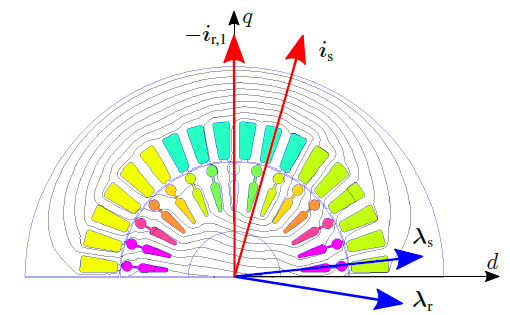
Figure 9: First iteration field solution. The rotor flux space vector does not lie along the \(d\)-axis of the adopted reference frame: the rotor current amplitude is not yet the correct value.
From the first iteration field solution, it is possible to compute the stator and rotor d- and q-axis flux linkages:
\[ \label{eq26} \begin{eqnarray}
\lambda_{sd} & = & L_s i_{sd} \\
\lambda_{sq} & = & L_s i_{sq} - M i_{sq} = L_{\sigma s} i_{sq} \\
\lambda_{rd} & = & M i_{rd} \\
\lambda_{rq} & = & L_r i_{rq} - M i_{rq} = L_{\sigma r} i_{rq}
\end{eqnarray} \]
and the stator and rotor leakage inductances can be isolated. The rotor current for the second iteration can be obtained elaborating (23), remembering (24):
\[ \label{eq27} \begin{eqnarray}
i_{rq} & =& -i_{sq} \left( 1-\frac{L_{\sigma r}}{L_r} \right) \simeq -i_{sq} \left( 1-\frac{L_{\sigma r}}{M} \right) \\
\rightarrow i_{rq} & \simeq & -i_{sq} \left( 1-\frac{\lambda_{rq}}{i_{sq}} \frac{i_{sd}}{\lambda_{rd}} \right)
\end{eqnarray} \]
then, the rotor current vector, applied in the second iteration is:
\[ \label{eq28} i_{r,2} =j \left( i_{sq} + \frac{\lambda_{rq,1}}{\lambda_{rd,1}} i_{sd}\right) \]
where \(\lambda_{rq,1}\) and \(\lambda_{rd,1}\) are the rotor flux linkages computed at the first iteration.
The points (\(\lambda_{rq,1}\), \(i_{rq,1}\)) and (\(\lambda_{rq,2}\), \(i_{rq,2}\)) represents a straight line in the plane (\(\lambda_{rq}\), \(i_{rq}\)).
The current \(i_{rq}\) to obtain \(\lambda_{rq} = 0\) is computed as:
\[ \label{eq29} i_{rq_3} = \frac{\lambda_{rq,2} i_{rq,1} − \lambda_{rq,1} i_{rq,2}}{\lambda_{rq,2} − \lambda_{rq,1}}\]
and the rotor current space vector applied in the third iteration is:
\[ \label{eq30} i_{r,3} = -j i_{rq,3} \]
The third iteration field solution is reported in Figure 10.
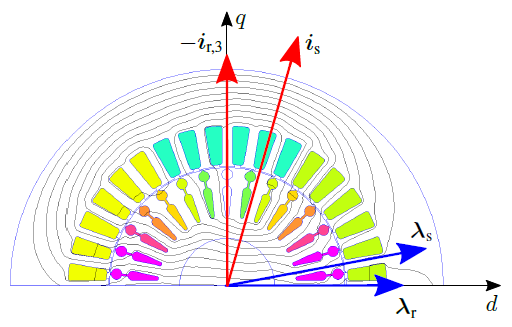
Figure 10: Third iteration field solution. The rotor flux space vector lies along the \(d\)-axis of the adopted reference frame: the rotor current amplitude has the correct value.
As can be noticed in the field solution in Figure 10, now, the flux lines inside the rotor are almost parallel to the d-axis of the adopted reference frame. This means that the rotor \(q\)-axis flux linkage is almost equal to zero.
The partial results of the iterative procedure are graphically reported in Figure 11. The first interesting thing is that between the first and the third iteration current, the difference is rather slight, meaning that the torque and the flux linkages, computed at the first step are very similar to the third. This result is generally true for open slot IMs, whereas for closed slots motors the difference between the first and third step current is remarkable.
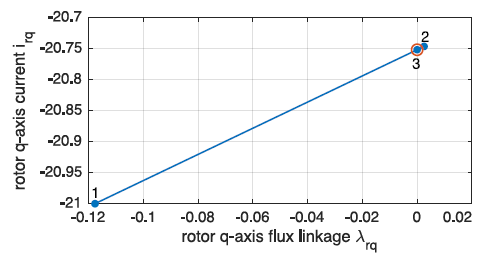
Figure 11: Iterative process results at each iteration. At the third step, the rotor \(q\)-axis flux linkage is almost equal to zero.
Once the inverse-Γ model condition (\(\lambda_{rq} = 0\)) has been verified, the rotor first harmonic current is considered to be correctly imposed in the third step of the procedure. From the last field solution in Figure 10, besides the stator and rotor flux linkages, also the torque and the rotor angular frequency can be derived using (22) and (20).
5 Discussion
The method presented in this article shows a rapid prediction technique of the rotor induced current when the stator current is known in the \(dq\) reference frame. The procedure adopts the RFO reference frame, in which the rotor current lies along the \(q\)-axis. The amplitude of the rotor current is computed using a FEA-based iterative procedure, which ends when \(\lambda_{rq} = 0\).
The procedure is particularly suitable for current driven controlled IMs, following the same analysis strategy of synchronous motors. However, this procedure can be extended to grid connected machines and the skewing can be easily considered coupling the model with the multi-slice theory [4, 7–9].
Thanks to the link with the \(dq\) RFO model, the mapping process is very intuitive and completely similar to the synchronous machines. This makes the procedure described in this article suitable for the analysis of variable speed IMs [10].
In different works by the authors, the model has been “complicated” to consider also the effect of the harmonics in the additional iron losses, cage losses and torque ripple. The analysis can be extended to several position during the on load operation, for the evaluation of the instantaneous torque and the flux density pulsation in each mesh element.
In the code attached to this article, the base Rotor Field Oriented Analysis (RFOA) procedure is implemented with the sinusoidal current distribution along the rotor periphery and the single position analysis. The example reported concerns a grid connected induction motor: the magnetizing current \(i_{sd}\) is obtained from the no-load test and the on-load behavior using the RFOA, increasing the \(q\)-axis current. If one excludes the no-load part, the analysis method is ready for current controlled IMs with the rotor Field Oriented Control (FOC) or for a complete mapping in the plane (\(i_{sd}\), \(i_{sq}\)), to study the variable speed working trajectories.
Acronyms
FE Finite Element.
FEA Finite Element Analysis.
FOC Field Oriented Control
IM Induction Motor.
MMF Magneto Motive Force.
MS Magneto-Static.
RFO Rotor Field Oriented
RFOA Rotor Field Oriented Analysis
TD Time Domain.
Symbols
\(B_{3ph1}\) Three-phase fundamental air-gap flux density [T]
\(L_{mr}\) Rotor magnetizing inductance [H]
\(L_{ms}\) Stator magnetizing inductance [H]
\(L_{s}\) Stator three-phase synchronous inductance [H]
\(L_{r}\) Rotor three-phase synchronous inductance [H]
\(L_{t}\) Transient leakage inductance [H]
\(L_{\sigma s}\) Stator leakage inductance [H]
\(L_{\sigma r}\) Rotor leakage inductance [H]
\(L_{\varphi}\) inverse-Γ equivalent circuit magnetizing inductance [H]
\(M\) three-phase synchronous mutual inductance between stator and rotor [H]
\(D_i\) Inner diameter [mm]
\(L_{stk}\) Stack length [mm]
\(N_r\) Rotor equivalent series conductors per phase
\(N_s\) Stator series conductors per phase
\(P_{Jr}\) Rotor first harmonic current Joule losses [W]
\(Q_r\) Rotor number of slots
\(R_s\) Stator phase resistance [Ω]
\(R_r\) Rotor phase resistance [Ω]
\(T_{dq}\) \(dq\) model torque [N m]
\(\alpha_r^e\) Rotor electrical slot angle [rad]
\(k_{wr}\) Rotor equivalent winding factor
\(k_{ws}\) Stator winding factor
\(\mu_o\) Vacuum permeability [H/m]
\(\omega_s\) Stator angular frequency [1/s]
\(\omega_{sl}\) Slip angular frequency [1/s]
\(\omega_{me}\) Rotor elecrical speed in the stationary frame [1/s]
\(\vec{i}_{s}\) Stator current space vector [A]
\(\vec{i}_{r}\) Rotor current space vector [A]
\(\vec{v}_{s}\) Stator voltage space vector [V]
\(g\) Air-gap [mm]
\(p\) The number of pole pairs
\(s\) Slip of the fundamental field with respect the rotor [-]
References
[1] Antero Arkkio. Analysis of induction motors based on the numerical solution of the magnetic field and circuit equations, 1987-12-18.
[2] L. Alberti, N. Bianchi, and S. Bolognani. A very rapid prediction of im performance combining analytical and finite-element analysis. IEEE Transactions on Industry Applications, 44(5):1505–1512, Sep. 2008.
[3] G. R. Slemon. Modelling of inductance machines for electric drives. In Conference Record of the 1988 IEEE Industry Applications Society Annual Meeting, pages 111–115 vol.1, Oct 1988.
[4] M. Carbonieri, N. Bianchi, and L. Alberti. Direct analysis of induction motor using finite element. In 2018 IEEE Energy Conversion Congress and Exposition (ECCE), pages 277–283, Sep. 2018.
[5] M. Carbonieri, N. Bianchi, and L. Alberti. A fast and direct analysis of three-phase induction motors using finite element. In 2018 XIII International Conference on Electrical Machines (ICEM), pages 18–24, Sep. 2018.
[6] T.A. Lipo and Wisconsin Power Electronics Research Center. Introduction to AC Machine Design. Wisconsin Power Electronics Research Center, University of Wisconsin, 1996.
[7] M. Carbonieri, N. Bianchi, and L. Alberti. Induction motor analysis using magnetostatic finite element simulations considering skewing. In 2019 IEEE International Electric Machines Drives Conference (IEMDC), pages 147–153, May 2019.
[8] S. Williamson and C. I. McClay. The effect of axial variations in saturation due to skew on induction motor equivalent-circuit parameters. In IAS ’97. Conference Record of the 1997 IEEE Industry Applications Conference Thirty-Second IAS Annual Meeting, volume 1, pages 120–127 vol.1, Oct 1997.
[9] A. Tenhunen and A. Arkkio. Modelling of induction machines with skewed rotor slots. IEE Proceedings - Electric Power Applications, 148(1):45–50, Jan 2001.
[10] M. Carbonieri, N. Bianchi, and L. Alberti. Induction motor mapping using rotor field-oriented analysis technique. In 2019 IEEE Energy Conversion Congress and Exposition (ECCE), pages 2321–2328, Sep. 2019.
| File | Last modified | Size |
|---|---|---|
| IM_Code.zip | 2021-07-21 21:30 | 24Kb |
| Report.pdf | 2021-07-21 21:31 | 791Kb |